
यथा शिखा मयूराणाम् नागानां मणयो यथा |
तद्वद् वेदांगशास्त्राणाम् गणितं मूर्धनि स्थितं ||
( लगध : वेदांग ज्योतिषं :4) before 3500 B.C
[Like the crest of the peacocks, like the crest-jewels of the serpants, so does the lore of the mathematics stand at the head of all the lores forming the auxiliaries of the vedas]
------------------------------------------------------------------------------------------------
The Newton-Leibniz feud over priority of discovery of calculus is a famous episode in modern western mathematical history. That these two men, despite having many other inventiones/discoveries to their credit, fought over calculus itself lends an idea as to how important a discipline it is. Many of us, whose disciplines involve mathematics in some way,have experienced the utility of calculus during our education. It is almost an ubiquitous mathematical technique.
In this blog which i divide into 2 parts, I intend to summarise from various sources about how Indian mathematicians over the ages came very close to discovering calculus. In fact, they did use calculus, but in a limited sense of astronomy and did not extend it to general functional analysis.Due credit must be given to them for some of the greatest ideas they introduced for the first time in the history of mathematics like infinite series and error associated , numerical integration and infinitesimals. The euro-centric view tries to cast aside these as a mere footnote. This is a ridiculous situation.
While I provide the details about various mathematicians in the following paragraphs, I stick to the dates in history given according to modern research, by V.Lakshmikantham and S.Leela as opposed to euro-centric dates which always tries to push all Indian dates into A.D and hence prove that Indians learnt all things from greeks(although it should be appreciated that there was interaction and mutual learning between indians and greeks to some extent over the ages) .
For more information on this view of indian history see:
http://www.vnn.org/editorials/ET0003/ET14-5679.html
For more information on this view of indian history see:
http://www.vnn.org/editorials/ET0003/ET14-5679.html
Though there are so many contributions to the field of mathematics by Indians, in this blog i concentrate only on those aspects that involve calculus ideas. Astronomy was the main discipline for Indians although right from Aryabhatta's time we see chapters exclusively dedicated to mathematics too. In the course of tackling various problems in astronomy, elegant mathematical techniques were developed.
In this first part i will outline details about our mathematical history upto the point of Bhaskaracharya II. In the second part we will take up the medieval Kerala school of mathematics and their contributions.
Ideas of zero and infinity
 These two important concepts in mathematics were known from time immemorial in India in sanathana dharma (eg, anantam) and emphasised more by the later indian religions namely, buddhism(from c.1800BC) and jainism. The infinite brahman(ananta) as well as infinite cycle of yugas were the fundamentals of upanishads. zero was the part of the place value notation indicated in the vedic literature.
These two important concepts in mathematics were known from time immemorial in India in sanathana dharma (eg, anantam) and emphasised more by the later indian religions namely, buddhism(from c.1800BC) and jainism. The infinite brahman(ananta) as well as infinite cycle of yugas were the fundamentals of upanishads. zero was the part of the place value notation indicated in the vedic literature.
Buddhism's 'sunyavadham' and Jainism's five kinds of infinities also developed these concepts further. The idea of infinitesimals and limits often involve a variable approaching these two entities.
In this first part i will outline details about our mathematical history upto the point of Bhaskaracharya II. In the second part we will take up the medieval Kerala school of mathematics and their contributions.
Ideas of zero and infinity
 These two important concepts in mathematics were known from time immemorial in India in sanathana dharma (eg, anantam) and emphasised more by the later indian religions namely, buddhism(from c.1800BC) and jainism. The infinite brahman(ananta) as well as infinite cycle of yugas were the fundamentals of upanishads. zero was the part of the place value notation indicated in the vedic literature.
These two important concepts in mathematics were known from time immemorial in India in sanathana dharma (eg, anantam) and emphasised more by the later indian religions namely, buddhism(from c.1800BC) and jainism. The infinite brahman(ananta) as well as infinite cycle of yugas were the fundamentals of upanishads. zero was the part of the place value notation indicated in the vedic literature.Buddhism's 'sunyavadham' and Jainism's five kinds of infinities also developed these concepts further. The idea of infinitesimals and limits often involve a variable approaching these two entities.
Aryabhatta (born 2765 B.C) was one of the very important early mathematicians/astronomer who influenced later mathematicians for over the following 4000 years. He gave the value of π (pi) to be 3.1416 and mentioned that it is an approximate value. This value was remarkable for his age. Though it is not very clear as to how he arrived at this value, there are theories that he used a 256 sided polygon as an approximation to the circle. This has been disproved in a subsequent paper. There is also a theory that he used a 384 sided polygon ('crest of the peacock:Non-European roots of mathematics' and 'Geometry in Ancient and Medieval India'). These indicate that Aryabhatta had the insight of the limiting value of the perimeter of a N-gon to be the circumference of the inscribed circle.
He also introduced the notion of tatkalikagathi(instantaneous motion) while talking about the motion of moon and planets and expressed the instantaneous velocity of a heavenly body in the form of a basic differential equation. Aryabhatta and Brahmagupta(born 30 B.C) gave the formula pertaining to instantaneous motion as
 where u,v,w are the true longitude, mean longitude, mean anamoly respectively at any particular time and u' , v' , w' are the values of the respective quantities at a subsequent instant and e is the eccentricity or the sine of the greatest equation of the orbit. This was later expounded fully by Bhaskaracharya who writes:
where u,v,w are the true longitude, mean longitude, mean anamoly respectively at any particular time and u' , v' , w' are the values of the respective quantities at a subsequent instant and e is the eccentricity or the sine of the greatest equation of the orbit. This was later expounded fully by Bhaskaracharya who writes:
He also introduced the notion of tatkalikagathi(instantaneous motion) while talking about the motion of moon and planets and expressed the instantaneous velocity of a heavenly body in the form of a basic differential equation. Aryabhatta and Brahmagupta(born 30 B.C) gave the formula pertaining to instantaneous motion as
 where u,v,w are the true longitude, mean longitude, mean anamoly respectively at any particular time and u' , v' , w' are the values of the respective quantities at a subsequent instant and e is the eccentricity or the sine of the greatest equation of the orbit. This was later expounded fully by Bhaskaracharya who writes:
where u,v,w are the true longitude, mean longitude, mean anamoly respectively at any particular time and u' , v' , w' are the values of the respective quantities at a subsequent instant and e is the eccentricity or the sine of the greatest equation of the orbit. This was later expounded fully by Bhaskaracharya who writes:'to find the instantaneous velocity in longitude of the planet, the kotiphala is to be multiplied by the time rate of change of anomaly and divided by the radius, and the quotient thus obtained is to be added to or subtracted from the mean velocity of the planet according to its position in the six signs from the beginning of cancer or capricon'. Expressed in modern notation,
 where the symbols have their meaning like true longitude,mean longitude,anamoly,radius of epicycle,kotiphala etc.(which cannot be easily understood without a deeper knowledge in astronomy)
where the symbols have their meaning like true longitude,mean longitude,anamoly,radius of epicycle,kotiphala etc.(which cannot be easily understood without a deeper knowledge in astronomy)While dealing with this type of equation, Manjula(c.900 A.D) hit upon an important result in differential :
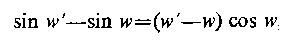 where (w'- w) is small.
where (w'- w) is small.Virasena(710-790A.D) uses the method of exhausion to find the volume of frustum of a cone in his Dhavala. If a and b are the diameters of the bigger and smaller bases, then he removes a cylinder of diameter b from the solid and cuts open the solid to form a wedge kind of solid. He then removes smaller and smaller pieces from it and through series summation arrives at the result. This is akin to techniques that Archimedes uses for the quadrature of parabola and other figures.
Bhaskaracharya(b. 1114 A.D)-(486A.D according to Lakshmikantham and Leela)-(well known as Bhaskara-II)gives the geometrical proof of the above result and uses it to calculate "the angle of position"(an important parameter in determining the position and velocity of planets).
In modern notation it is as follows:
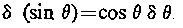
 Bhaskara-II expressed other important ideas of differential and integral calculus in his texts. He had a primitive notion of limit. In the second chapter 46th verse of Lilavathi, his well known mathematical treatise, he poses the following question and answer:
Bhaskara-II expressed other important ideas of differential and integral calculus in his texts. He had a primitive notion of limit. In the second chapter 46th verse of Lilavathi, his well known mathematical treatise, he poses the following question and answer:'What number is it, which multiplied by cipher and added to half itself and multiplied by three, and divided by cipher, amounts to the given number sixty three?'
The question may seem strange for a modern reader for we were all taught that dividing by zero is not allowed in operations. Here if we take a look at the answer given by bhaskara and the method he adopts to arrive at it, we can compare it to the notion of limits that we have today.
The answer given by him is 14. Let us look at the method. Do not operate with the zeros until the end. Write the expression and we finally cancel the zeros as shown.
 This is akin to:
This is akin to: The following two important results , which are wrongly attributed to later day european mathematicians such as Rolle were given by Bhaskaracharya.
The following two important results , which are wrongly attributed to later day european mathematicians such as Rolle were given by Bhaskaracharya.1. When a variable attains maximum value, its differential disappears.
2. When a planet is either in apogee or perigee, the equation of the centre vanishes, hence for some intermediate position, the increment of the equation of the centre(ie, differential in modern term) also vanishes.
The second one is the celebrated intermediate value theorem.
Bhaskara has up his sleeve some very ingenious numerical integration methods to find the volume and the surface area of a sphere. He first gave the correct formula for the volume of sphere in the indian subcontinent.
Methods Surface area of a sphere:
1. The first method is to divide the surface of the sphere into thin strips by drawing circles of increasing radius keeping one of the poles as the centre. This will result in latitude kind of circles on the surface. (See below)

Now area of each strip is found out by considering it as a rolled up trapezium.(Note that dimensions of the trapezium are known because while we draw the circles we measure the increasing radius in terms of arcs of sine, the table of which exists right from Aryabhatta's time).
This totalled up gives the surface area. Bhaskara concludes through explanation here that the area can be generalised as (circumference x diameter). The essence of this method is the idea of integration, though not presented in a numerical rather than the general way.
2. The second method is by dividing the sphere into lunes (vapras) as shown below and adding the areas.

The way Bhaskara indicates this method is interesting. He asks us to divide the sphere into parts that resemble natural divisions on the amalaka(myrobalan) fruit. Even through this method the consistent result of (circumference x diameter) is concluded. I do not wish to go into details here but a comprehensive description can be found in Sarasvati amma's book 'Geometry in Ancient and medieval India'.
Volume of sphere:
In the words of Bhaskara , " Consider on the surface of the sphere pyramidal excavations, each of a base of an unit area having unit sides and of a depth equal to the radius of the sphere, as many as the number of units of area on the sphere. The apices of these pyramid meet at the centre of the sphere. The sum of the volumes of the pyramids equals the volume of the sphere".
This idea is a 3 dimensional extension of the method to find circle's area when it was divided into triangles.
The next part will concentrate on Post Bhaskara II mathematics,mainly on the Kerala School of mathematics which gave some of the most brilliant results ever to humanity.
COURTESY: Various issues of Indian journal of history of science, 'Geometry in ancient and medieval india' by Saraswati Amma, 'Crest of peacock', 'Origin of mathematics'

Great article - very authoritative and as a European I can safely say that yes India does need to reclaim its contribution to this area of mathematics.
ReplyDeleteVenetia Ansell
The Sanskrit Literature Forum
www.venetiaansell.wordpress.com
Thank you Venetia for your comments. It is good to know a European's point of view on the subject too.
ReplyDeleteWell written article with convincing facts and relevant data.
ReplyDeleteSorry for being philosophical but whenever I come across such articles, I cant stop wondering why we stopped and everything was lost. But yes it is good that we are rediscovering and reclaiming now.
There might be several physical reasons for the halt or loss. But lack and ideological flexibility could be another reason. Ideology in science is like putting limits to ones thinking. I guess the definition of science is " to question" and we stopped questioning believing we had all the right answers . Yes a framework is necessary but you have to go beyond it every now and then to adapt to constantly changing times. I believe we are again at the same crossroads of science based on facts and ideology especially in medicine. We need to set aside our political and ideological differences and work concretely in the field of medicine and environment through sciencing (questioning).
Thanks for the comment prasaanna. There are other historical reasons too for the halt of science development in india after 16th century. First communication with the outside world was very less compared what scientists had at the same period in europe. This is more due to lack of common language too. Take the hypothetical situation that the developments had been exchanged between india and europe. Then more and more scholars would have been drawn into group efforts to improve on existing knowledge.India would also have participated in the scientific renaissance of the past 4 centuries(i feel this is a strong reason because till the 1600s europe too was at a similar level compared to india in science and technology). Another reason that comes to my mind is the constant fear of the muslim invasion and terror in the country. They destroyed many valuable texts and to an extent hindered progress. Well, i definitely agree with your point of rigidity in ideology that crept in and prevented much progress.
ReplyDeleteHope we are improving now,though i feel it is not upto the mark considering institutions like ceeri which is more of a money sink to our government than anything(though there are good institutions too).
Yes, certainly there are lot of positives now. The whole point of studying history is to learn from our mistakes. Now we need to work collectively with no inhibitions and boundaries.
ReplyDeleteHey Anand,
ReplyDeleteI knew most of it before. Obviously I did not do homework like you. I remember you discussing most of it with me.
I remember you mentioning Education System must change where in students must also be taught the origins and history of calculus and not just d(sin x) = cos x : which in my opinion completely makes sense.
And as far as the blog is concerned: Clearly expressed, neatly organized and thoroughly convincing. Keep it going.
To put it short: It is a rediscovery!
Did Bhaskara 2 contribute more to Calculus than Newton?Is there any book that describe the works of Bhaskara 2 in English? Any input on the subject would be highly appreciated.
ReplyDeleteBhaskara had ideas of infinitesimals but cannot be said to have used calculus. However, the Kerala mathematicians from Madhava till Jyeshtadeva and beyond significantly contributed to infinite series and calculus. There are English translations of Lilavati and Ganita yukti bhasa that give us an idea of infinitesimal calculus in India before it started appearing in Europe. Another very informative book by Dr. C. K. Raju discusses how calculus was transmitted from Kerala to Europe by Jesuit missionaries and influenced a chain of mathematicians there.
Delete